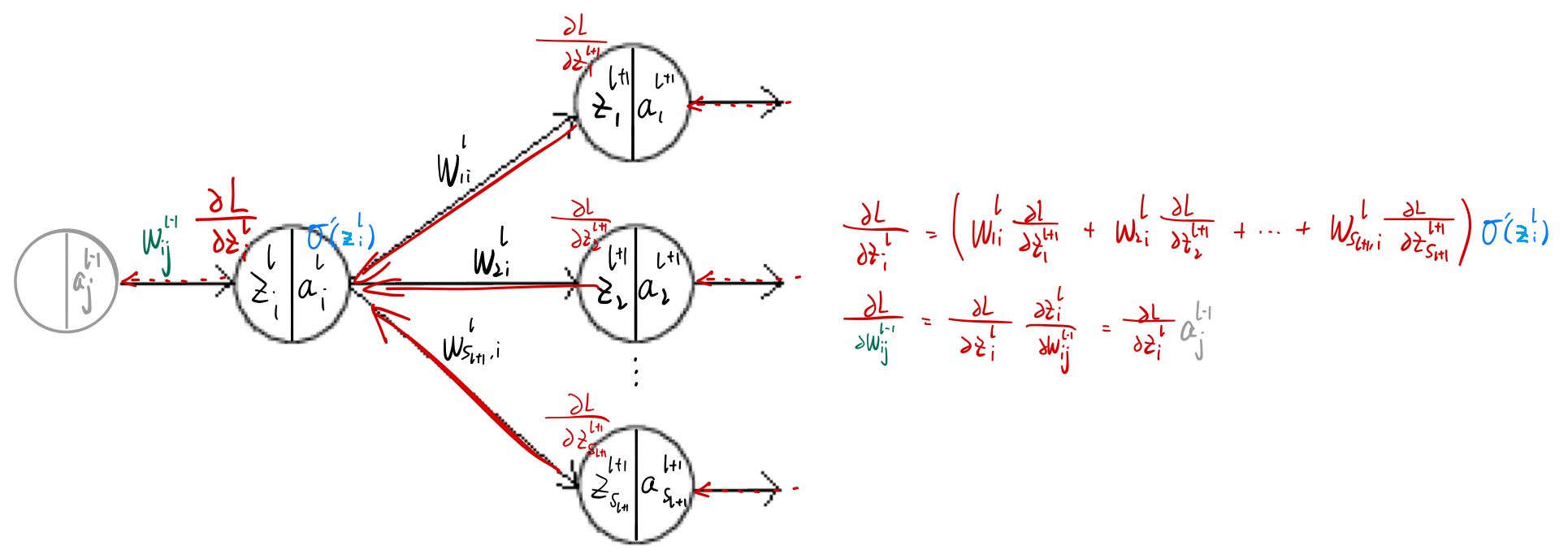
反向传播 简单介绍一下BP算法:
给定一个输入x x x h W , b ( x ) h_{W,b}(x) h W , b ( x ) W , b W,b W , b 根据标签值y y y 详细推导
相关符号定义:
网络的总层数设为n l n_l n l n l − 1 n_l-1 n l − 1 l l l [ 1 , n l ] [1,n_l] [ 1 , n l ] 1 1 1 n l n_l n l 网络权重和偏置( W , b ) : = ( W 1 , b 1 , W 2 , b 2 , . . . , W n l − 1 , b n l − 1 ) (W,b):=(W^1,b^1,W^2,b^2,...,W^{n_l-1},b^{n_l-1}) ( W , b ) : = ( W 1 , b 1 , W 2 , b 2 , . . . , W n l − 1 , b n l − 1 ) W i , j l W_{i,j}^l W i , j l l l l j j j l + 1 l+1 l + 1 i i i b i l b_i^l b i l l + 1 l+1 l + 1 i i i 记z i l z_i^l z i l l l l i i i z i l = ∑ j = 1 S l − 1 ( W i j l − 1 a j l − 1 ) + b i l − 1 z_i^{l}=\sum\limits_{j=1}^{S_{l-1}}(W_{ij}^{l-1}a_j^{l-1})+b_i^{l-1} z i l = j = 1 ∑ S l − 1 ( W i j l − 1 a j l − 1 ) + b i l − 1 a i l a_i^l a i l l l l i i i 记S l S_l S l l l l 以第l l l a l − 1 ∈ R S l − 1 × 1 a^{l-1}\in R^{S_{l-1}\times 1} a l − 1 ∈ R S l − 1 × 1 W l − 1 = [ W 11 l − 1 W 21 l − 1 ⋯ W S l , 1 l − 1 W 12 l − 1 W 22 l − 1 ⋯ W S l , 2 l − 1 ⋮ ⋮ ⋱ ⋮ W 1 , S l − 1 l − 1 W 2 , S l − 1 l − 1 ⋯ W S l , S l − 1 l − 1 ] ∈ R S l − 1 × S l W^{l-1}=\begin{bmatrix}W_{11}^{l-1}&W_{21}^{l-1}&\cdots&W_{S_l,1}^{l-1}\\W_{12}^{l-1}&W_{22}^{l-1}&\cdots&W_{S_l,2}^{l-1}\\\vdots&\vdots&\ddots&\vdots\\W_{1,S_{l-1}}^{l-1}&W_{2,S_{l-1}}^{l-1}&\cdots&W_{S_l,S_{l-1}}^{l-1}\end{bmatrix}\in R^{S_{l-1}\times S_l} W l − 1 = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ W 1 1 l − 1 W 1 2 l − 1 ⋮ W 1 , S l − 1 l − 1 W 2 1 l − 1 W 2 2 l − 1 ⋮ W 2 , S l − 1 l − 1 ⋯ ⋯ ⋱ ⋯ W S l , 1 l − 1 W S l , 2 l − 1 ⋮ W S l , S l − 1 l − 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ∈ R S l − 1 × S l b l − 1 ∈ R S l × 1 b^{l-1}\in R^{S_l\times 1} b l − 1 ∈ R S l × 1 l l l a l = σ ( z l ) = σ ( ( W l − 1 ) T a l − 1 + b l − 1 ) ∈ R S l × 1 a^l=\sigma(z^l)=\sigma((W^{l-1})^Ta^{l-1}+b^{l-1})\in R^{S_l\times 1} a l = σ ( z l ) = σ ( ( W l − 1 ) T a l − 1 + b l − 1 ) ∈ R S l × 1 σ ( ⋅ ) \sigma(·) σ ( ⋅ ) L = 1 2 ∥ h W , b ( x ) − y ∥ 2 L=\frac{1}{2}\|h_{W,b}(x)-y\|^2 L = 2 1 ∥ h W , b ( x ) − y ∥ 2 z z z
输出层∂ L ∂ z i n l = ∂ ∂ z i n l ( 1 2 ∑ j = 1 S n l ( a j n l − y j ) 2 ) = ( a i n l − y i ) ∂ a i n l ∂ z i n l = ( a i n l − y i ) σ ′ ( z i n l ) \frac{\partial L}{\partial z_i^{n_l}}=\frac{\partial}{\partial z_i^{n_l}}(\frac{1}{2}\sum\limits_{j=1}^{S_{n_l}}(a_j^{n_l}-y_j)^2)=(a_i^{n_l}-y_i)\frac{\partial a_i^{n_l}}{\partial z_i^{n_l}}=(a_i^{n_l}-y_i)\sigma^{\prime}(z_i^{n_l}) ∂ z i n l ∂ L = ∂ z i n l ∂ ( 2 1 j = 1 ∑ S n l ( a j n l − y j ) 2 ) = ( a i n l − y i ) ∂ z i n l ∂ a i n l = ( a i n l − y i ) σ ′ ( z i n l ) 非输出层∂ L ∂ z i n l − 1 = ∂ L ∂ z 1 n l ∂ z 1 n l ∂ z i n l − 1 + . . . + ∂ L ∂ z S n l n l ∂ z S n l n l ∂ z i n l − 1 = ∑ j = 1 S n l ( ∂ L ∂ z j n l ∂ z j n l ∂ z i n l − 1 ) = ∑ j = 1 S n l ( ∂ L ∂ z j n l W j i n l − 1 σ ′ ( z i n l − 1 ) ) \frac{\partial L}{\partial z_i^{n_l-1}}=\frac{\partial L}{\partial z_1^{n_l}}\frac{\partial z_1^{n_l}}{\partial z_i^{n_l-1}}+...+\frac{\partial L}{\partial z_{S_{n_l}}^{n_l}}\frac{\partial z_{S_{n_l}}^{n_l}}{\partial z_i^{n_l-1}}=\sum\limits_{j=1}^{S_{n_l}}(\frac{\partial L}{\partial z_j^{n_l}}\frac{\partial z_j^{n_l}}{\partial z_i^{n_l-1}})=\sum\limits_{j=1}^{S_{n_l}}(\frac{\partial L}{\partial z_j^{n_l}}W_{ji}^{n_l-1}\sigma^{\prime}(z_i^{n_l-1})) ∂ z i n l − 1 ∂ L = ∂ z 1 n l ∂ L ∂ z i n l − 1 ∂ z 1 n l + . . . + ∂ z S n l n l ∂ L ∂ z i n l − 1 ∂ z S n l n l = j = 1 ∑ S n l ( ∂ z j n l ∂ L ∂ z i n l − 1 ∂ z j n l ) = j = 1 ∑ S n l ( ∂ z j n l ∂ L W j i n l − 1 σ ′ ( z i n l − 1 ) ) z j n l = W j 1 n l − 1 σ ( z 1 n l − 1 ) + . . . + W j , S n l − 1 n l − 1 σ ( z S n l − 1 n l − 1 ) + b j n l − 1 z_j^{n_l}=W_{j1}^{n_l-1}\sigma(z_1^{n_l-1})+...+W_{j,S_{n_l-1}}^{n_l-1}\sigma(z_{S_{n_l-1}}^{n_l-1})+b_j^{n_l-1} z j n l = W j 1 n l − 1 σ ( z 1 n l − 1 ) + . . . + W j , S n l − 1 n l − 1 σ ( z S n l − 1 n l − 1 ) + b j n l − 1 l l l l ∈ { 2 , . . . , n l − 1 } l\in \{2,...,n_l-1\} l ∈ { 2 , . . . , n l − 1 } ∂ L ∂ z i l = ∑ j = 1 S l + 1 ( ∂ L ∂ z j l + 1 W j i l ) σ ′ ( z i l ) \frac{\partial L}{\partial z_i^l}=\sum\limits_{j=1}^{S_{l+1}}(\frac{\partial L}{\partial z_j^{l+1}}W_{ji}^{l})\sigma^{\prime}(z_i^l) ∂ z i l ∂ L = j = 1 ∑ S l + 1 ( ∂ z j l + 1 ∂ L W j i l ) σ ′ ( z i l ) 现在可以轻松求解∂ L ∂ W i j l = ∂ L ∂ z i l + 1 ∂ z i l + 1 ∂ W i j l = ∂ L ∂ z i l + 1 a j l \frac{\partial L}{\partial W_{ij}^l}=\frac{\partial L}{\partial z_i^{l+1}}\frac{\partial z_i^{l+1}}{\partial W_{ij}^l}=\frac{\partial L}{\partial z_i^{l+1}}a_j^l ∂ W i j l ∂ L = ∂ z i l + 1 ∂ L ∂ W i j l ∂ z i l + 1 = ∂ z i l + 1 ∂ L a j l ∂ L ∂ b i l = ∂ L ∂ z i l + 1 ∂ z i l + 1 ∂ b i l = ∂ L ∂ z i l + 1 1 \frac{\partial L}{\partial b_i^l}=\frac{\partial L}{\partial z_i^{l+1}}\frac{\partial z_i^{l+1}}{\partial b_i^l}=\frac{\partial L}{\partial z_i^{l+1}}1 ∂ b i l ∂ L = ∂ z i l + 1 ∂ L ∂ b i l ∂ z i l + 1 = ∂ z i l + 1 ∂ L 1
以上全部改写为矩阵形式,有:∂ L ∂ z n l = ( a n l − y ) ⊙ σ ′ ( z n l ) ∈ R S n l × 1 \frac{\partial L}{\partial z^{n_l}}=(a^{n_l}-y)\odot\sigma^{\prime}(z^{n_l})\in R^{S_{n_l}\times 1} ∂ z n l ∂ L = ( a n l − y ) ⊙ σ ′ ( z n l ) ∈ R S n l × 1 ⊙ \odot ⊙ ∂ L ∂ z n l − 1 = ( W n l − 1 ∂ L ∂ z n l ) ⊙ σ ′ ( z n l − 1 ) ∈ R S n l − 1 × 1 \frac{\partial L}{\partial z^{n_l-1}}=(W^{n_l-1}\frac{\partial L}{\partial z^{n_l}})\odot\sigma^{\prime}(z^{n_l-1})\in R^{S_{n_l-1}\times 1} ∂ z n l − 1 ∂ L = ( W n l − 1 ∂ z n l ∂ L ) ⊙ σ ′ ( z n l − 1 ) ∈ R S n l − 1 × 1 ∂ L ∂ z l = ( W l ∂ L ∂ z l + 1 ) ⊙ σ ′ ( z l ) ∈ R S l × 1 \frac{\partial L}{\partial z^l}=(W^l\frac{\partial L}{\partial z^{l+1}})\odot\sigma^{\prime}(z^l)\in R^{S_l\times 1} ∂ z l ∂ L = ( W l ∂ z l + 1 ∂ L ) ⊙ σ ′ ( z l ) ∈ R S l × 1 l = 1 , . . . , n l − 1 l=1,...,n_l-1 l = 1 , . . . , n l − 1
进一步,有:∂ L ∂ W l = [ ∂ L ∂ W 11 l ∂ L ∂ W 21 l ⋯ ∂ L ∂ W S l + 1 , 1 l ∂ L ∂ W 12 l ∂ L ∂ W 22 l ⋯ ∂ L ∂ W S l + 1 , 2 l ⋮ ⋮ ⋱ ⋮ ∂ L ∂ W 1 , S l l ∂ L ∂ W 2 , S l l ⋯ ∂ L ∂ W S l + 1 , S l l ] = [ ∂ L ∂ z 1 l + 1 a 1 l ∂ L ∂ z 2 l + 1 a 1 l ⋯ ∂ L ∂ z S l + 1 l + 1 a 1 l ∂ L ∂ z 1 l + 1 a 2 l ∂ L ∂ z 2 l + 1 a 2 l ⋯ ∂ L ∂ z S l + 1 l + 1 a 2 l ⋮ ⋮ ⋱ ⋮ ∂ L ∂ z 1 l + 1 a S l l ∂ L ∂ z 2 l + 1 a S l l ⋯ ∂ L ∂ z S l + 1 l + 1 a S l l ] = a l ( ∂ L ∂ z l + 1 ) T ∈ R S l × S l + 1 \frac{\partial L}{\partial W^l}=\begin{bmatrix}\frac{\partial L}{\partial W_{11}^{l}}&\frac{\partial L}{\partial W_{21}^{l}}&\cdots&\frac{\partial L}{\partial W_{S_{l+1},1}^{l}}\\\frac{\partial L}{\partial W_{12}^{l}}&\frac{\partial L}{\partial W_{22}^{l}}&\cdots&\frac{\partial L}{\partial W_{S_{l+1},2}^{l}}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial L}{\partial W_{1,S_{l}}^{l}}&\frac{\partial L}{\partial W_{2,S_{l}}^{l}}&\cdots&\frac{\partial L}{\partial W_{S_{l+1},S_{l}}^{l}}\end{bmatrix}=\begin{bmatrix}\frac{\partial L}{\partial z_{1}^{l+1}}a_{1}^l&\frac{\partial L}{\partial z_{2}^{l+1}}a_{1}^l&\cdots&\frac{\partial L}{\partial z_{S_{l+1}}^{l+1}}a_{1}^l\\\frac{\partial L}{\partial z_{1}^{l+1}}a_{2}^l&\frac{\partial L}{\partial z_{2}^{l+1}}a_{2}^l&\cdots&\frac{\partial L}{\partial z_{S_{l+1}}^{l+1}}a_{2}^l\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial L}{\partial z_{1}^{l+1}}a_{S_l}^l&\frac{\partial L}{\partial z_{2}^{l+1}}a_{S_l}^l&\cdots&\frac{\partial L}{\partial z_{S_{l+1}}^{l+1}}a_{S_l}^l\end{bmatrix}=a^l(\frac{\partial L}{\partial z^{l+1}})^T\in R^{S_l\times S_{l+1}} ∂ W l ∂ L = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∂ W 1 1 l ∂ L ∂ W 1 2 l ∂ L ⋮ ∂ W 1 , S l l ∂ L ∂ W 2 1 l ∂ L ∂ W 2 2 l ∂ L ⋮ ∂ W 2 , S l l ∂ L ⋯ ⋯ ⋱ ⋯ ∂ W S l + 1 , 1 l ∂ L ∂ W S l + 1 , 2 l ∂ L ⋮ ∂ W S l + 1 , S l l ∂ L ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∂ z 1 l + 1 ∂ L a 1 l ∂ z 1 l + 1 ∂ L a 2 l ⋮ ∂ z 1 l + 1 ∂ L a S l l ∂ z 2 l + 1 ∂ L a 1 l ∂ z 2 l + 1 ∂ L a 2 l ⋮ ∂ z 2 l + 1 ∂ L a S l l ⋯ ⋯ ⋱ ⋯ ∂ z S l + 1 l + 1 ∂ L a 1 l ∂ z S l + 1 l + 1 ∂ L a 2 l ⋮ ∂ z S l + 1 l + 1 ∂ L a S l l ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = a l ( ∂ z l + 1 ∂ L ) T ∈ R S l × S l + 1 ∂ L ∂ b l = ∂ L ∂ z l + 1 ∈ R S l + 1 × 1 \frac{\partial L}{\partial b^l}=\frac{\partial L}{\partial z^{l+1}}\in R^{S_{l+1}\times 1} ∂ b l ∂ L = ∂ z l + 1 ∂ L ∈ R S l + 1 × 1
Pytorch标量对矩阵求导 举个例子,∂ t r ( A X B X ) ∂ X = A T X T B T + B T X T A T \frac{\partial tr(AXBX)}{\partial X}=A^TX^TB^T+B^TX^TA^T ∂ X ∂ t r ( A X B X ) = A T X T B T + B T X T A T 矩阵求导术 ”得出)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 >>> import torch as pt>>> X=pt.arange(12 ,dtype=pt.float32).view(3 ,4 ) >>> _=X.requires_grad_(True ) >>> A=pt.rand(4 ,3 ) >>> B=pt.rand(4 ,3 )>>> out=pt.trace(A.mm(X).mm(B).mm(X)) >>> out.backward() >>> X.grad tensor([[35.3752 , 34.2365 , 9.8990 , 22.8047 ], [31.8588 , 32.2588 , 8.7556 , 17.3359 ], [24.6398 , 21.3645 , 6.5890 , 17.4973 ]]) >>> pt.t(A).mm(pt.t(X)).mm(pt.t(B))+pt.t(B).mm(pt.t(X)).mm(pt.t(A)) tensor([[35.3752 , 34.2365 , 9.8990 , 22.8047 ], [31.8587 , 32.2588 , 8.7556 , 17.3359 ], [24.6398 , 21.3645 , 6.5890 , 17.4973 ]], grad_fn=<AddBackward0>)
线性回归模型 简要回顾:
线性回归预测模型定义为y ^ = w 1 x 1 + w 2 x 2 + . . . + w n x n + b \hat{y}=w_1x_1+w_2x_2+...+w_nx_n+b y ^ = w 1 x 1 + w 2 x 2 + . . . + w n x n + b w = [ w 1 , . . . , w n ] T , b w=[w_1,...,w_n]^T,b w = [ w 1 , . . . , w n ] T , b x = [ x 1 , . . . , x n ] T x=[x_1,...,x_n]^T x = [ x 1 , . . . , x n ] T m m m Y ^ = w T X + b \hat{Y}=w^TX+b Y ^ = w T X + b X = [ x ( 1 ) , . . . , x ( m ) ] X=[x^{(1)},...,x^{(m)}] X = [ x ( 1 ) , . . . , x ( m ) ] Y ^ = [ y ^ ( 1 ) , . . . , y ^ ( m ) ] \hat{Y}=[\hat{y}^{(1)},...,\hat{y}^{(m)}] Y ^ = [ y ^ ( 1 ) , . . . , y ^ ( m ) ] Y = [ y ( 1 ) , . . . , y ( m ) ] Y=[y^{(1)},...,y^{(m)}] Y = [ y ( 1 ) , . . . , y ( m ) ] i i i l ( w , b ) ( i ) = 1 2 ( y ^ ( i ) − y ( i ) ) 2 l_{(w,b)}^{(i)}=\frac{1}{2}(\hat{y}^{(i)}-y^{(i)})^2 l ( w , b ) ( i ) = 2 1 ( y ^ ( i ) − y ( i ) ) 2 m m m L ( w , b ) = 1 m ∑ i = 1 m l ( w , b ) ( i ) L_{(w,b)}=\frac{1}{m}\sum\limits_{i=1}^ml_{(w,b)}^{(i)} L ( w , b ) = m 1 i = 1 ∑ m l ( w , b ) ( i ) w ∗ , b ∗ = arg min w , b L ( w , b ) = arg min w , b 1 2 m ∥ Y ^ − Y ∥ 2 2 w^*,b^*=\arg\min\limits_{w,b}L_{(w,b)}=\arg\min\limits_{w,b}\frac{1}{2m}\|\hat{Y}-Y\|_2^2 w ∗ , b ∗ = arg w , b min L ( w , b ) = arg w , b min 2 m 1 ∥ Y ^ − Y ∥ 2 2 { w ← w − r ∂ L ( w , b ) ∂ w b ← b − r ∂ L ( w , b ) ∂ b \begin{cases}w\leftarrow w-r\frac{\partial L_{(w,b)}}{\partial w} \\ b\leftarrow b-r\frac{\partial L_{(w,b)}}{\partial b}\end{cases} { w ← w − r ∂ w ∂ L ( w , b ) b ← b − r ∂ b ∂ L ( w , b ) r r r
编程实现(核心步骤):
定义网络模型w T X + b w^TX+b w T X + b 定义损失函数1 2 m ∥ ( w T X + b ) − Y ∥ 2 \frac{1}{2m}\|(w^TX+b)-Y\|^2 2 m 1 ∥ ( w T X + b ) − Y ∥ 2 定义优化算法grad属性中(记得反向传播前清零),梯度下降要做的就是用模型参数减去这些导数值,然后将结果作为参数的新值 准备数据 定义模型、损失和优化算法 训练 附(简洁实现) 假设真实权重为w = [ 2 , 3.4 ] T w=[2,3.4]^T w = [ 2 , 3 . 4 ] T b = 4.2 b=4.2 b = 4 . 2 Y = w T X + b + ϵ Y=w^TX+b+\epsilon Y = w T X + b + ϵ ϵ \epsilon ϵ
1 2 3 4 5 6 7 8 import numpy as nptrue_w=np.array([[2 ],[3.4 ]]) true_b=np.array([4.2 ]) samples_num=1000 X=np.random.randn(len (true_w),samples_num) Y=true_w.T@X+true_b Y+=np.random.normal(0 ,0.01 ,size=Y.shape)
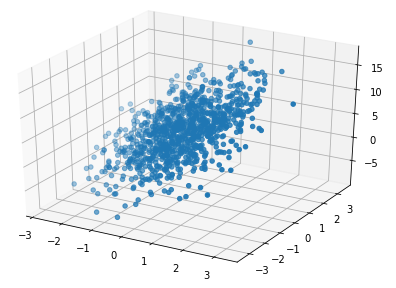
(三维)可视化数据:
1 2 3 4 5 6 import matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3Dax=Axes3D(plt.gcf()) data=np.vstack((X,Y)) ax.scatter(*data) plt.show()
在上述“核心步骤”中已经解释过了,直接看代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 import torch as ptdef linear_regress (X,w,b ): return pt.t(w).mm(X)+b def square_loss (Y_hat,Y ): return pt.sum ((Y_hat-Y)**2 /2 ) def sgd (params,learn_rate,batch_size ): for param in params: param.data-=(learn_rate*param.grad/batch_size)
在开始训练前还要准备一些东西:训练数据的批量(batch)数据生成器、模型参数的初始化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 X=pt.from_numpy(X).to(pt.float32) Y=pt.from_numpy(Y).to(pt.float32) def data_iter (X,Y,batch_size ): n=X.shape[1 ] ind=np.arange(n) np.random.shuffle(ind) for i in range (0 ,n,batch_size): j=pt.LongTensor(ind[i:min (i+batch_size,n)]) yield X.index_select(1 ,j),Y.index_select(1 ,j) def init_params (): w=pt.tensor(np.random.normal(0 ,0.01 ,(X.shape[0 ],1 )),dtype=pt.float32) b=pt.zeros(1 ,dtype=pt.float32) w.requires_grad_(requires_grad=True ) b.requires_grad_(requires_grad=True ) return w,b
开始训练:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 num_epoches=5 learn_rate=0.03 batch_size=10 w,b=init_params() for epoch in range (num_epoches): for mini_X,mini_Y in data_iter(X,Y,batch_size): mini_Y_hat=linear_regress(mini_X,w,b) loss=square_loss(mini_Y_hat,mini_Y) loss.backward() sgd((w,b),learn_rate,batch_size) _=w.grad.data.zero_() _=b.grad.data.zero_() print ('epoch=%d,loss=%f' %(epoch+1 ,square_loss(linear_regress(X,w,b),Y))) print ('-' *22 )print ('w:' ,w.data) print ('b:' ,b.data)'''OUTPUT epoch=1,loss=32.869465 epoch=2,loss=0.122995 epoch=3,loss=0.054227 epoch=4,loss=0.054130 epoch=5,loss=0.054148 ---------------------- w: tensor([[2.0000], [3.3990]]) b: tensor([4.1995]) '''
比较简单,直接看代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 import torch as ptimport numpy as npdef gen_data (true_w,true_b,samples_num ): '''参数:真实的权重(列向量),偏置(标量),训练数据个数(列代表样本)。Ndarray对象 返回:训练数据(dxn),值(标签,1xn)。Tensor/float32对象''' X=np.random.randn(len (true_w),samples_num) Y=true_w.T@X+true_b Y+=np.random.normal(0 ,0.01 ,size=Y.shape) return pt.from_numpy(X).to(pt.float32),pt.from_numpy(Y).to(pt.float32) import torch.utils.data as Datadef data_iter (features,labels,batch_size ): dataset = Data.TensorDataset(features, labels) iteration=Data.DataLoader(dataset, batch_size, shuffle=True ) return iteration import torch.nn as nnlinearNet=lambda input_num: nn.Sequential(nn.Linear(input_num,1 )) loss=nn.MSELoss() import torch.optim as optimoptimize=lambda params,lr:optim.SGD(params,lr=lr) from torch.nn import initepoches=10 true_w=np.array([[2 ],[3.4 ]]) true_b=4.2 samples_num=1000 batch_size=10 train_X,train_Y=gen_data(true_w,true_b,samples_num) net=linearNet(len (true_w)) _=init.normal_(net[0 ].weight, mean=0 , std=0.01 ) _=init.constant_(net[0 ].bias, val=0 ) opt=optimize(net.parameters(),0.01 ) for epoch in range (epoches): for mini_X,mini_Y in data_iter(pt.t(train_X),pt.t(train_Y),batch_size): out=net(mini_X) l=loss(out,mini_Y.view(-1 ,1 )) l.backward() opt.step() net.zero_grad() print ('epoch=%d,loss=%f' %(epoch+1 ,l.item())) print ('-' *21 )print (net[0 ].weight.data)print (net[0 ].bias.data)'''OUTPUT epoch=1,loss=0.395253 epoch=2,loss=0.015482 epoch=3,loss=0.000321 epoch=4,loss=0.000112 epoch=5,loss=0.000151 epoch=6,loss=0.000066 epoch=7,loss=0.000070 epoch=8,loss=0.000097 epoch=9,loss=0.000113 epoch=10,loss=0.000144 --------------------- tensor([[2.0000, 3.3993]]) tensor([4.2006]) '''
Softmax分类模型 简要回顾(注意从本段开始,我会稍稍规范化latex公式的书写,会用大写和加粗来区别表示标量x x x x \mathbf{x} x X \mathbf{X} X
介绍Softmax(多)分类模型之前先介绍一下Logistic(二)分类模型,Logistic分类模型的目的在于找到一个超平面w x + b = 0 \mathbf{w}\mathbf{x}+b=0 w x + b = 0 w = [ w 1 , . . . , w n ] ∈ R 1 × n \mathbf{w}=[w_1,...,w_n]\in R^{1\times n} w = [ w 1 , . . . , w n ] ∈ R 1 × n x = [ x 1 , . . . , x n ] T ∈ R n × 1 \mathbf{x}=[x_1,...,x_n]^T\in R^{n\times 1} x = [ x 1 , . . . , x n ] T ∈ R n × 1 b ∈ R b\in R b ∈ R n n n y y y y = 1 y=1 y = 1 y = 0 y=0 y = 0 y ^ = h w , b ( x ) = σ ( w x + b ) \hat{y}=h_{\mathbf{w},b}(\mathbf{x})=\sigma(\mathbf{w}\mathbf{x}+b) y ^ = h w , b ( x ) = σ ( w x + b ) σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ ( x ) = 1 + e − x 1 σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) \sigma^{\prime}(x)=\sigma(x)(1-\sigma(x)) σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) σ ( ⋅ ) \sigma(·) σ ( ⋅ ) [ 0 , 1 ] [0,1] [ 0 , 1 ] y ^ \hat{y} y ^ x \mathbf{x} x P ( y = 1 ∣ x , w , b ) P(y=1|\mathbf{x},\mathbf{w},b) P ( y = 1 ∣ x , w , b ) 1 − y ^ 1-\hat{y} 1 − y ^ x \mathbf{x} x x \mathbf{x} x y = { 1 , 0 } y=\{1,0\} y = { 1 , 0 } P ( y ∣ x , w , b ) = σ ( w x + b ) y ( 1 − σ ( w x + b ) ) 1 − y P(y|\mathbf{x},\mathbf{w},b)=\sigma(\mathbf{w}\mathbf{x}+b)^{y}(1-\sigma(\mathbf{w}\mathbf{x}+b))^{1-y} P ( y ∣ x , w , b ) = σ ( w x + b ) y ( 1 − σ ( w x + b ) ) 1 − y w \mathbf{w} w b b b m m m { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) } \{(\mathbf{x}^{(1)},y^{(1)}),(\mathbf{x}^{(2)},y^{(2)}),...,(\mathbf{x}^{(m)},y^{(m)})\} { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) } L w , b ′ = ∏ i = 1 m P ( y ( i ) ∣ x ( i ) , w , b ) = ∏ i = 1 m [ h w , b ( x ( i ) ) y ( i ) ( 1 − h w , b ( x ( i ) ) ) 1 − y ( i ) ] L_{\mathbf{w},b}^{'}=\prod\limits_{i=1}^m P(y^{(i)}|\mathbf{x^{(i)}},\mathbf{w},b)=\prod\limits_{i=1}^m[h_{\mathbf{w},b}(\mathbf{x}^{(i)})^{y^{(i)}}(1-h_{\mathbf{w},b}(\mathbf{x}^{(i)}))^{1-y^{(i)}}] L w , b ′ = i = 1 ∏ m P ( y ( i ) ∣ x ( i ) , w , b ) = i = 1 ∏ m [ h w , b ( x ( i ) ) y ( i ) ( 1 − h w , b ( x ( i ) ) ) 1 − y ( i ) ] L w , b = − 1 m ln L w , b ′ = − 1 m ∑ i = 1 m [ y ( i ) ln ( h w , b ( x ( i ) ) ) + ( 1 − y ( i ) ) ln ( 1 − h w , b ( x ( i ) ) ) ] = − 1 m ∑ i = 1 m [ y ( i ) ln ( y ^ ( i ) ) + ( 1 − y ( i ) ) ln ( 1 − y ^ ( i ) ) ] L_{\mathbf{w},b}=-\frac{1}{m}\ln L_{\mathbf{w},b}^{'}=-\frac{1}{m}\sum\limits_{i=1}^m[y^{(i)}\ln(h_{\mathbf{w},b}(\mathbf{x}^{(i)}))+(1-y^{(i)})\ln(1-h_{\mathbf{w},b}(\mathbf{x}^{(i)}))]=-\frac{1}{m}\sum\limits_{i=1}^m[y^{(i)}\ln(\hat{y}^{(i)})+(1-y^{(i)})\ln(1-\hat{y}^{(i)})] L w , b = − m 1 ln L w , b ′ = − m 1 i = 1 ∑ m [ y ( i ) ln ( h w , b ( x ( i ) ) ) + ( 1 − y ( i ) ) ln ( 1 − h w , b ( x ( i ) ) ) ] = − m 1 i = 1 ∑ m [ y ( i ) ln ( y ^ ( i ) ) + ( 1 − y ( i ) ) ln ( 1 − y ^ ( i ) ) ] (某些地方还会看到另一种写法,若记f ( x ) = w x + b f(\mathbf{x})=\mathbf{w}\mathbf{x}+b f ( x ) = w x + b L w , b = 1 m ∑ i = 1 m [ y ( i ) ln ( 1 + e − f ( x ( i ) ) ) + ( 1 − y ( i ) ) ln ( 1 + e f ( x ( i ) ) ) ] = 1 m ∑ i = 1 m ln ( 1 + e ( − 1 ) y ( i ) f ( x ( i ) ) ) L_{\mathbf{w},b}=\frac{1}{m}\sum\limits_{i=1}^m[y^{(i)}\ln(1+e^{-f(\mathbf{x}^{(i)})})+(1-y^{(i)})\ln(1+e^{f(\mathbf{x}^{(i)})})]=\frac{1}{m}\sum\limits_{i=1}^m\ln(1+e^{(-1)^{y^{(i)}}f(\mathbf{x}^{(i)})}) L w , b = m 1 i = 1 ∑ m [ y ( i ) ln ( 1 + e − f ( x ( i ) ) ) + ( 1 − y ( i ) ) ln ( 1 + e f ( x ( i ) ) ) ] = m 1 i = 1 ∑ m ln ( 1 + e ( − 1 ) y ( i ) f ( x ( i ) ) ) 1 1 1 0 0 0 1 1 1 − 1 -1 − 1 L w , b = 1 m ∑ i = 1 m ln ( 1 + e − y ( i ) f ( x ( i ) ) ) L_{\mathbf{w},b}=\frac{1}{m}\sum\limits_{i=1}^m\ln(1+e^{-y^{(i)}f(\mathbf{x}^{(i)})}) L w , b = m 1 i = 1 ∑ m ln ( 1 + e − y ( i ) f ( x ( i ) ) )
Softmax(多)分类是Logistic(二)分类的一个推广,或者说后者是前者的一个特例。和线性回归模型相比,Softmax也是一个单层神经网络,只不过输出层有多个节点(等于类别数)并且加了一个sigmoid激活函数。相比于二分类寻找单个超平面,多分类会寻找多个超平面用于分割多种(大于2)不同的类别:w 1 x + b 1 = 0 \mathbf{w}_1\mathbf{x}+b_1=0 w 1 x + b 1 = 0 w 2 x + b 2 = 0 \mathbf{w}_2\mathbf{x}+b_2=0 w 2 x + b 2 = 0 w x + b = 0 \mathbf{w}\mathbf{x}+b=0 w x + b = 0 θ = [ b , w ] T ∈ R ( n + 1 ) × 1 \boldsymbol{\theta}=[b,\mathbf{w}]^T\in R^{(n+1)\times 1} θ = [ b , w ] T ∈ R ( n + 1 ) × 1 x = [ 1 , x 1 , . . . , x n ] ∈ R ( n + 1 ) × 1 \mathbf{x}=[1,x_1,...,x_n]\in R^{(n+1)\times 1} x = [ 1 , x 1 , . . . , x n ] ∈ R ( n + 1 ) × 1 θ T x = 0 \boldsymbol{\theta}^T\mathbf{x}=0 θ T x = 0 k k k Θ = [ θ 1 , θ 2 , . . . , θ k ] ∈ R ( n + 1 ) × k \Theta=[\boldsymbol{\theta}_1,\boldsymbol{\theta}_2,...,\boldsymbol{\theta}_k]\in R^{(n+1)\times k} Θ = [ θ 1 , θ 2 , . . . , θ k ] ∈ R ( n + 1 ) × k y ^ = h Θ ( x ) = softmax ( Θ T x ) ∈ R k × 1 \hat{\mathbf{y}}=h_\Theta(\mathbf{x})=\textbf{softmax}(\Theta^T\mathbf{x})\in R^{k\times 1} y ^ = h Θ ( x ) = softmax ( Θ T x ) ∈ R k × 1 softmax ( x ) = exp ( x ) ∑ exp ( x ) \textbf{softmax}(\mathbf{x})=\frac{\exp(\mathbf{x})}{\sum\exp(\mathbf{x})} softmax ( x ) = ∑ e x p ( x ) e x p ( x ) m m m L Θ = − 1 m ∑ i = 1 m ∑ j = 1 k y j ( i ) ln ( y ^ j ( i ) ) L_\Theta=-\frac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^k\mathbf{y}_j^{(i)}\ln(\hat{\mathbf{y}}_j^{(i)}) L Θ = − m 1 i = 1 ∑ m j = 1 ∑ k y j ( i ) ln ( y ^ j ( i ) ) y ( i ) \mathbf{y}^{(i)} y ( i ) x ( i ) \mathbf{x}^{(i)} x ( i ) y ( i ) y^{(i)} y ( i )
Softmax(多)分类是Logistic(二)分类的一个推广,或者说后者是前者的一个特例。和线性回归模型相比,Softmax也是一个单层神经网络,只不过输出层有多个节点(等于类别数)并且加了一个sigmoid激活函数。相比于二分类寻找单个超平面,多分类会寻找多个超平面用于分割多种(大于2)不同的类别:w 1 x + b 1 = 0 \mathbf{w}_1\mathbf{x}+b_1=0 w 1 x + b 1 = 0 w 2 x + b 2 = 0 \mathbf{w}_2\mathbf{x}+b_2=0 w 2 x + b 2 = 0 w x + b = 0 \mathbf{w}\mathbf{x}+b=0 w x + b = 0 θ = [ b , w ] T ∈ R ( n + 1 ) × 1 \boldsymbol{\theta}=[b,\mathbf{w}]^T\in R^{(n+1)\times 1} θ = [ b , w ] T ∈ R ( n + 1 ) × 1 x = [ 1 , x 1 , . . . , x n ] ∈ R ( n + 1 ) × 1 \mathbf{x}=[1,x_1,...,x_n]\in R^{(n+1)\times 1} x = [ 1 , x 1 , . . . , x n ] ∈ R ( n + 1 ) × 1 θ T x = 0 \boldsymbol{\theta}^T\mathbf{x}=0 θ T x = 0 k k k Θ = [ θ 1 , θ 2 , . . . , θ k ] ∈ R ( n + 1 ) × k \Theta=[\boldsymbol{\theta}_1,\boldsymbol{\theta}_2,...,\boldsymbol{\theta}_k]\in R^{(n+1)\times k} Θ = [ θ 1 , θ 2 , . . . , θ k ] ∈ R ( n + 1 ) × k y ^ = h Θ ( x ) = 1 ∑ i = 1 k e θ i T x [ e θ 1 T x e θ 2 T x ⋮ e θ k T x ] = softmax ( Θ T x ) ≡ [ P ( y = 1 ∣ x , Θ ) P ( y = 2 ∣ x , Θ ) ⋮ P ( y = k ∣ x , Θ ) ] ∈ R k × 1 \hat{\mathbf{y}}=h_\Theta(\mathbf{x})=\frac{1}{\sum\limits_{i=1}^ke^{\boldsymbol{\theta}_i^T\mathbf{x}}}\begin{bmatrix}e^{\boldsymbol{\theta}_1^T\mathbf{x}}\\e^{\boldsymbol{\theta}_2^T\mathbf{x}}\\\vdots\\e^{\boldsymbol{\theta}_k^T\mathbf{x}}\end{bmatrix}=\textbf{softmax}(\Theta^T\mathbf{x})\equiv \begin{bmatrix}P(y=1|\mathbf{x},\Theta)\\P(y=2|\mathbf{x},\Theta)\\\vdots\\P(y=k|\mathbf{x},\Theta)\end{bmatrix}\in R^{k\times 1} y ^ = h Θ ( x ) = i = 1 ∑ k e θ i T x 1 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ e θ 1 T x e θ 2 T x ⋮ e θ k T x ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = softmax ( Θ T x ) ≡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ P ( y = 1 ∣ x , Θ ) P ( y = 2 ∣ x , Θ ) ⋮ P ( y = k ∣ x , Θ ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ∈ R k × 1 softmax ( x ) = exp ( x ) ∑ exp ( x ) \textbf{softmax}(\mathbf{x})=\frac{\exp(\mathbf{x})}{\sum\exp(\mathbf{x})} softmax ( x ) = ∑ e x p ( x ) e x p ( x )
和Logistic分类的联系:假设k = 2 k=2 k = 2 h Θ ( x ) = [ e θ 1 T x e θ 1 T x + e θ 2 T x e θ 2 T x e θ 1 T x + e θ 2 T x ] = [ 1 1 + e ( θ 2 − θ 1 ) T x ≡ v 1 − v ] h_\Theta(\mathbf{x})=\begin{bmatrix}\frac{e^{\boldsymbol{\theta}_1^T\mathbf{x}}}{e^{\boldsymbol{\theta}_1^T\mathbf{x}}+e^{\boldsymbol{\theta}_2^T\mathbf{x}}}\\\frac{e^{\boldsymbol{\theta}_2^T\mathbf{x}}}{e^{\boldsymbol{\theta}_1^T\mathbf{x}}+e^{\boldsymbol{\theta}_2^T\mathbf{x}}}\end{bmatrix}=\begin{bmatrix}\frac{1}{1+e^{(\boldsymbol{\theta}_2-\boldsymbol{\theta}_1)^T\mathbf{x}}}\equiv v\\1-v\end{bmatrix} h Θ ( x ) = ⎣ ⎢ ⎡ e θ 1 T x + e θ 2 T x e θ 1 T x e θ 1 T x + e θ 2 T x e θ 2 T x ⎦ ⎥ ⎤ = [ 1 + e ( θ 2 − θ 1 ) T x 1 ≡ v 1 − v ] v v v σ ( ( θ 2 − θ 1 ) T x ) \sigma((\boldsymbol{\theta}_2-\boldsymbol{\theta}_1)^T\mathbf{x}) σ ( ( θ 2 − θ 1 ) T x )
至于Softmax分类模型的损失函数,对于m m m L Θ = − 1 m ∑ i = 1 m ∑ j = 1 k [ I { y ( i ) = j } ln e θ j T x ( i ) ∑ l = 1 k e θ l T x ( i ) ] L_\Theta=-\frac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^k[I\{y^{(i)}=j\}\ln\frac{e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}}{\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}}] L Θ = − m 1 i = 1 ∑ m j = 1 ∑ k [ I { y ( i ) = j } ln l = 1 ∑ k e θ l T x ( i ) e θ j T x ( i ) ] I I I I { condition } = { 1 , if condition is true 0 , if condition is false I\{\text{condition}\}=\begin{cases}1,\text{if condition is true}\\0,\text{if condition is false}\end{cases} I { condition } = { 1 , if condition is true 0 , if condition is false
参考书[2]错误纠正
对书中P29求导部分的更正:∇ θ q L Θ = − 1 m ∑ i = 1 m ∑ j = 1 k [ I { y ( i ) = j } ∂ ∂ θ q ( ln e θ j T x ( i ) ∑ l = 1 k e θ l T x ( i ) ) ] \nabla_{\boldsymbol{\theta}_q}^{L_\Theta}=-\frac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^k[I\{y^{(i)}=j\}\frac{\partial}{\partial \boldsymbol{\theta}_q}(\ln\frac{e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}}{\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}})] ∇ θ q L Θ = − m 1 i = 1 ∑ m j = 1 ∑ k [ I { y ( i ) = j } ∂ θ q ∂ ( ln l = 1 ∑ k e θ l T x ( i ) e θ j T x ( i ) ) ] ln \ln ln d d x ln ( u ) = 1 u d u d x \frac{d}{dx}\ln(u)=\frac{1}{u}\frac{du}{dx} d x d ln ( u ) = u 1 d x d u ( u v ) ′ = u ′ v − u v ′ v 2 (\frac{u}{v})^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{v^2} ( v u ) ′ = v 2 u ′ v − u v ′ ∂ e θ j T x ( i ) ∂ θ q = { e θ j T x ( i ) x ( i ) , q = j 0 , q ≠ j = e θ j T x ( i ) I { q = j } x ( i ) \frac{\partial e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}}{\partial \boldsymbol{\theta}_q}=\begin{cases}e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}\mathbf{x}^{(i)},q=j\\0,q\ne j\end{cases}=e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}I\{q=j\}\mathbf{x}^{(i)} ∂ θ q ∂ e θ j T x ( i ) = { e θ j T x ( i ) x ( i ) , q = j 0 , q = j = e θ j T x ( i ) I { q = j } x ( i ) ∇ θ q L Θ = − 1 m ∑ i = 1 m ∑ j = 1 k [ I { y ( i ) = j } ∑ l = 1 k e θ l T x ( i ) e θ j T x ( i ) e θ j T x ( i ) I { q = j } x ( i ) ∑ l = 1 k e θ l T x ( i ) − e θ j T x ( i ) x ( i ) e θ q T x ( i ) ( ∑ l = 1 k e θ l T x ( i ) ) 2 ] = − 1 m ∑ i = 1 m ∑ j = 1 k [ I { y ( i ) = j } I { q = j } ∑ l = 1 k e θ l T x ( i ) − e θ q T x ( i ) ∑ l = 1 k e θ l T x ( i ) x ( i ) ] = − 1 m ∑ i = 1 m [ I { q = y ( i ) } ∑ l = 1 k e θ l T x ( i ) − e θ q T x ( i ) ∑ l = 1 k e θ l T x ( i ) x ( i ) ] = − 1 m ∑ i = 1 m [ ( I { y ( i ) = q } − P ( y = q ∣ x ( i ) , Θ ) ) x ( i ) ] \nabla_{\boldsymbol{\theta}_q}^{L_\Theta}=-\frac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^k[I\{y^{(i)}=j\}\frac{\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}}{e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}}\frac{e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}I\{q=j\}\mathbf{x}^{(i)}\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}-e^{\boldsymbol{\theta}_j^T\mathbf{x}^{(i)}}\mathbf{x}^{(i)}e^{\boldsymbol{\theta}_q^T\mathbf{x}^{(i)}}}{(\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}})^2}]=-\frac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^k[I\{y^{(i)}=j\}\frac{I\{q=j\}\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}-e^{\boldsymbol{\theta}_q^T\mathbf{x}^{(i)}}}{\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}}\mathbf{x}^{(i)}]=-\frac{1}{m}\sum\limits_{i=1}^m[\frac{I\{q=y^{(i)}\}\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}-e^{\boldsymbol{\theta}_q^T\mathbf{x}^{(i)}}}{\sum\limits_{l=1}^ke^{\boldsymbol{\theta}_l^T\mathbf{x}^{(i)}}}\mathbf{x}^{(i)}]=-\frac{1}{m}\sum\limits_{i=1}^m[(I\{y^{(i)}=q\}-P(y=q|\mathbf{x}^{(i)},\Theta))\mathbf{x}^{(i)}] ∇ θ q L Θ = − m 1 i = 1 ∑ m j = 1 ∑ k [ I { y ( i ) = j } e θ j T x ( i ) l = 1 ∑ k e θ l T x ( i ) ( l = 1 ∑ k e θ l T x ( i ) ) 2 e θ j T x ( i ) I { q = j } x ( i ) l = 1 ∑ k e θ l T x ( i ) − e θ j T x ( i ) x ( i ) e θ q T x ( i ) ] = − m 1 i = 1 ∑ m j = 1 ∑ k [ I { y ( i ) = j } l = 1 ∑ k e θ l T x ( i ) I { q = j } l = 1 ∑ k e θ l T x ( i ) − e θ q T x ( i ) x ( i ) ] = − m 1 i = 1 ∑ m [ l = 1 ∑ k e θ l T x ( i ) I { q = y ( i ) } l = 1 ∑ k e θ l T x ( i ) − e θ q T x ( i ) x ( i ) ] = − m 1 i = 1 ∑ m [ ( I { y ( i ) = q } − P ( y = q ∣ x ( i ) , Θ ) ) x ( i ) ]
上述给出的Softmax分类模型的损失其实就是所谓的交叉熵损失,下面给出简洁且常见的表示形式,对于单样本,其k k k y ^ \hat{\mathbf{y}} y ^ y \mathbf{y} y y y y l Θ = − ∑ i = 1 k y i ln ( y ^ i ) l_\Theta=-\sum\limits_{i=1}^k\mathbf{y}_i\ln(\hat{\mathbf{y}}_i) l Θ = − i = 1 ∑ k y i ln ( y ^ i ) m m m L Θ = − 1 m ∑ i = 1 m ∑ j = 1 k y j ( i ) ln ( y ^ j ( i ) ) = − 1 m ∑ i = 1 m ( y ( i ) ) T ln ( y ^ ( i ) ) = − 1 m t r ( [ y ( 1 ) , . . . , y ( m ) ] T [ ln ( y ^ ( 1 ) ) , . . . , ln ( y ^ ( m ) ) ] ) L_\Theta=-\frac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^k\mathbf{y}_j^{(i)}\ln(\hat{\mathbf{y}}_j^{(i)})=-\frac{1}{m}\sum\limits_{i=1}^m(\mathbf{y}^{(i)})^T\ln(\hat{\mathbf{y}}^{(i)})=-\frac{1}{m}tr([\mathbf{y}^{(1)},...,\mathbf{y}^{(m)}]^T[\ln(\hat{\mathbf{y}}^{(1)}),...,\ln(\hat{\mathbf{y}}^{(m)})]) L Θ = − m 1 i = 1 ∑ m j = 1 ∑ k y j ( i ) ln ( y ^ j ( i ) ) = − m 1 i = 1 ∑ m ( y ( i ) ) T ln ( y ^ ( i ) ) = − m 1 t r ( [ y ( 1 ) , . . . , y ( m ) ] T [ ln ( y ^ ( 1 ) ) , . . . , ln ( y ^ ( m ) ) ] ) y ^ ( i ) \hat{\mathbf{y}}^{(i)} y ^ ( i ) y ( i ) \mathbf{y}^{(i)} y ( i ) i ∈ { 1 , . . . , m } i\in \{1,...,m\} i ∈ { 1 , . . . , m } f ( x ) = Θ T x f(\mathbf{x})=\Theta^T\mathbf{x} f ( x ) = Θ T x L Θ = − 1 m ∑ i = 1 m ∑ j = 1 k y j ( i ) ln ( e f ( x ( i ) ) j ∑ l = 1 k e f ( x ( i ) ) l ) L_\Theta=-\frac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^k\mathbf{y}_j^{(i)}\ln(\frac{e^{f(\mathbf{x}^{(i)})_j}}{\sum_{l=1}^ke^{f(\mathbf{x}^{(i)})_l}}) L Θ = − m 1 i = 1 ∑ m j = 1 ∑ k y j ( i ) ln ( ∑ l = 1 k e f ( x ( i ) ) l e f ( x ( i ) ) j ) y ( i ) \mathbf{y}^{(i)} y ( i ) y ( i ) y^{(i)} y ( i ) y ( i ) \mathbf{y}^{(i)} y ( i ) y ( i ) y^{(i)} y ( i ) 1 m ∑ i = 1 m ln ( 1 + ∑ l = 1 , l ≠ y ( i ) k e f ( x ( i ) ) l e f ( x ( i ) ) y ( i ) ) \frac{1}{m}\sum\limits_{i=1}^m\ln(1+\frac{\sum_{l=1,l\ne y^{(i)}}^ke^{f(\mathbf{x}^{(i)})_l}}{e^{f(\mathbf{x}^{(i)})_{y^{(i)}}}}) m 1 i = 1 ∑ m ln ( 1 + e f ( x ( i ) ) y ( i ) ∑ l = 1 , l = y ( i ) k e f ( x ( i ) ) l )
编程实现:
和线性回归示例一样,需要定义网络模型、定义损失函数、定义优化算法三大步骤。(批量m m m X ∈ R d × m \mathbf{X}\in R^{d\times m} X ∈ R d × m k k k Y ^ k × m = softmax ( W d × k T X d × m + B k × 1 ) \hat{\mathbf{Y}}_{k\times m}=\textbf{softmax}(\mathbf{W}_{d\times k}^T\mathbf{X}_{d\times m}+\mathbf{B}_{k\times 1}) Y ^ k × m = softmax ( W d × k T X d × m + B k × 1 ) softmax \textbf{softmax} softmax L W , B = − 1 m t r ( Y k × m T ln ( Y ^ k × m ) ) L_{W,B}=-\frac{1}{m}tr(\mathbf{Y}_{k\times m}^T\ln(\hat{\mathbf{Y}}_{k\times m})) L W , B = − m 1 t r ( Y k × m T ln ( Y ^ k × m ) )
准备数据 定义模型、损失和优化函数 训练 附(简洁实现) 首先通过torchvision.datasets模块获取Fashion-MNIST图像分类数据集,并利用transforms.ToTensor()函数将所有图像数据(numpy对象,[ 0 − 255 ] [0-255] [ 0 − 2 5 5 ] Uint8类型)转换成Tensor张量对象,且数值为介于[ 0.0 − 1.0 ] [0.0-1.0] [ 0 . 0 − 1 . 0 ] torch.float32类型:
1 2 3 4 5 6 7 8 9 10 11 12 13 import torchvisionimport torchvision.transforms as transformsmnist_train = torchvision.datasets.FashionMNIST(root='./data/FashionMNIST' , train=True , download=True , transform=transforms.ToTensor()) mnist_test = torchvision.datasets.FashionMNIST(root='./data/FashionMNIST' , train=False , download=True , transform=transforms.ToTensor()) print (len (mnist_train),len (mnist_test))feature,label=mnist_train[0 ] print (feature.shape,label) '''OUTPUT 60000 10000 torch.Size([1, 28, 28]) 9 '''
训练集和测试集中的每个类别的图像数分别为6,000和1,000,统共10个类别,为t-shirt(T恤)、trouser(裤子)、pullover(套衫)、dress(连衣裙)、coat(外套)、sandal(凉鞋)、shirt(衬衫)、sneaker(运动鞋)、bag(包)和ankle boot(短靴),因此总计有70,000张图像。图像数据的形状为(c,h,w),三个符号分别代表通道数、高度、宽度,根据上述输出可知,此处图像是单通道的
可视化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import matplotlib.pyplot as pltdef get_fashion_mnist_labels (labels ): text_labels = ['t-shirt' , 'trouser' , 'pullover' , 'dress' , 'coat' , 'sandal' , 'shirt' , 'sneaker' , 'bag' , 'ankle boot' ] return [text_labels[int (i)] for i in labels] def show_fashion_mnist (images,labels ): for i in range (len (images)): ax=plt.subplot(1 ,len (images),i+1 ) plt.imshow(np.squeeze(images[i].numpy()).reshape(28 ,28 ),cmap='gray' ) plt.xlabel(get_fashion_mnist_labels([labels[i]])[0 ]) plt.xticks([]) plt.yticks([]) plt.show() X, y = [], [] for i in range (5 ): X.append(mnist_train[i][0 ]) y.append(mnist_train[i][1 ]) show_fashion_mnist(X,y)
首先定义前向传播时要用到的softmax函数:
1 2 3 def softmax (WX ): WX=WX.exp() return WX/WX.sum ()
再定义模型、损失和优化函数:
1 2 3 4 5 6 7 8 9 10 11 12 def softmax_classify (X,W,B ): return softmax(pt.t(W).mm(X)+B) def cross_loss (Y_hat,Y ): return -pt.trace(pt.t(Y).mm(pt.log(Y_hat))) def sgd (params,learn_rate,batch_sise ): for param in params: param.data-=(learn_rate*param.grad/batch_size)
在训练前还要准备一些东西:批量数据生成器、one-hot编码以及参数初始化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import timebatch_size = 256 num_workers = 4 train_iter = pt.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True , num_workers=num_workers) test_iter = pt.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False , num_workers=num_workers) start = time.time() for X, y in train_iter: continue print ('%.2f sec' % (time.time() - start))def to_onehot (labels,N ): return (pt.arange(N).view(N,1 )==labels).to(pt.float32) def init_params (d,k ): W=pt.tensor(np.random.normal(0 ,0.01 ,(d,k)),dtype=pt.float32) B=pt.zeros(k,1 ,dtype=pt.float32) W.requires_grad_(requires_grad=True ) B.requires_grad_(requires_grad=True ) return W,B
为了评判模型在测试集上的性能,在每一轮epoch结束后都会计算预测准确率,对于批量测试数据,网络的输出Y ^ \hat{\mathbf{Y}} Y ^ Y \mathbf{Y} Y Y ^ \hat{\mathbf{Y}} Y ^ ( Y ^ . a r g m a x ( d i m = 0 ) = = Y . a r g m a x ( d i m = 0 ) ) . m e a n ( ) (\hat{\mathbf{Y}}.argmax(dim=0)==\mathbf{Y}.argmax(dim=0)).mean() ( Y ^ . a r g m a x ( d i m = 0 ) = = Y . a r g m a x ( d i m = 0 ) ) . m e a n ( )
1 2 3 4 5 6 7 8 9 10 11 def acc (Y_hat,Y ): return (Y_hat.argmax(dim=0 )==Y.argmax(dim=0 )).float ().mean().item() def calc_accuracy (data_iter, net_with_wb ): acc_sum, n = 0.0 , 0 for X, y in data_iter: acc_sum += (net_with_wb(pt.t(X.view(-1 ,784 ))).argmax(dim=0 )==y).float ().sum ().item() n += len (y) return acc_sum / n
开始训练:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from functools import partialstart_time=time.time() epoches=10 learn_rate=0.1 W,B=init_params(784 ,10 ) for epoch in range (epoches): for mini_samples,mini_labels in train_iter: mini_X=pt.t(mini_samples.view(-1 ,784 )) mini_Y=to_onehot(mini_labels,10 ) mini_Y_hat=softmax_classify(mini_X,W,B) loss=cross_loss(mini_Y_hat,mini_Y) loss.backward() sgd((W,B),learn_rate,batch_size) _=W.grad.data.zero_() _=B.grad.data.zero_() print ('epoch=%d,train_loss=%f,test_accuracy=%f' %(epoch+1 ,loss.data.item(),calc_accuracy(test_iter,partial(softmax_classify,W=W,B=B)))) print ('Time: %f' %(time.time()-start_time))'''OUTPUT epoch=1,train_loss=513.109375,test_accuracy=0.795100 epoch=2,train_loss=505.963837,test_accuracy=0.811600 epoch=3,train_loss=506.121246,test_accuracy=0.819600 epoch=4,train_loss=499.465485,test_accuracy=0.821300 epoch=5,train_loss=491.453918,test_accuracy=0.823300 epoch=6,train_loss=500.663055,test_accuracy=0.826000 epoch=7,train_loss=496.945709,test_accuracy=0.820800 epoch=8,train_loss=493.426422,test_accuracy=0.830900 epoch=9,train_loss=493.445496,test_accuracy=0.829300 epoch=10,train_loss=494.146027,test_accuracy=0.825700 Time: 33.636117 '''
编写预测函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 def predict (images,true_labels ): t=pt.cat(images,0 ) t=t.view(t.shape[0 ],-1 ) y=softmax_classify(pt.t(t),W,B).argmax(dim=0 ) print ('预测结果:' ) show_fashion_mnist(images,y) print ('真实标签:' ,get_fashion_mnist_labels(true_labels)) X, y = [], [] for i in pt.randint(0 ,10000 ,(8 ,)): X.append(mnist_test[i][0 ]) y.append(mnist_test[i][1 ]) predict(X,y)
比较简单,直接看代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 import torch as ptimport numpy as npbatch_size=128 num_inputs=784 num_outputs=10 train_iter,test_iter=load_data_fashion_mnist(batch_size,root='./data/FashionMNIST' ) import torch.nn as nnnet=nn.Sequential(FlattenLayer(),nn.Linear(num_inputs,num_outputs)) loss=nn.CrossEntropyLoss() optimizer=pt.optim.SGD(net.parameters(), lr=0.1 ) from torch.nn import init_=init.normal_(net[1 ].weight, mean=0 , std=0.01 ) _=init.constant_(net[1 ].bias, val=0 ) num_epochs = 5 train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None , None , optimizer)
上述代码用到了几个别人写好的功能函数 (后面还会用到,写在d2l.py中,作为模块调用):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 import torchimport torchvisionimport sysdef load_data_fashion_mnist (batch_size, resize=None , root='~/Datasets/FashionMNIST' ): """Download the fashion mnist dataset and then load into memory.""" trans = [] if resize: trans.append(torchvision.transforms.Resize(size=resize)) trans.append(torchvision.transforms.ToTensor()) transform = torchvision.transforms.Compose(trans) mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True , download=True , transform=transform) mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False , download=True , transform=transform) if sys.platform.startswith('win' ): num_workers = 4 else : num_workers = 6 train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True , num_workers=num_workers) test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False , num_workers=num_workers) return train_iter, test_iter class FlattenLayer (torch.nn.Module): def __init__ (self ): super (FlattenLayer, self).__init__() def forward (self, x ): return x.view(x.shape[0 ], -1 ) def sgd (params, lr, batch_size ): for param in params: param.data -= lr * param.grad / batch_size def evaluate_accuracy_ch3 (data_iter, net ): acc_sum, n = 0.0 , 0 for X, y in data_iter: acc_sum += (net(X).argmax(dim=1 ) == y).float ().sum ().item() n += y.shape[0 ] return acc_sum / n def train_ch3 (net, train_iter, test_iter, loss, num_epochs, batch_size, params=None , lr=None , optimizer=None ): for epoch in range (num_epochs): train_l_sum, train_acc_sum, n = 0.0 , 0.0 , 0 for X, y in train_iter: y_hat = net(X) l = loss(y_hat, y).sum () if optimizer is not None : optimizer.zero_grad() elif params is not None and params[0 ].grad is not None : for param in params: param.grad.data.zero_() l.backward() if optimizer is None : sgd(params, lr, batch_size) else : optimizer.step() train_l_sum += l.item() train_acc_sum += (y_hat.argmax(dim=1 ) == y).sum ().item() n += y.shape[0 ] test_acc = evaluate_accuracy_ch3(test_iter, net) print ('epoch %d, loss %.4f, train acc %.3f, test acc %.3f' % (epoch + 1 , train_l_sum / n, train_acc_sum / n, test_acc))
MLP多层感知器 简要回顾:
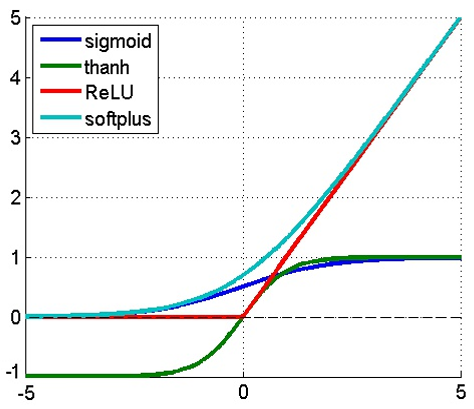
和线性回归、Softmax多分类相比,MLP增加了隐藏层的概念(实现了对输入空间的非线性映射+输出层线性判别分析)。给定批量n n n l l l Z l = ( W l − 1 ) T A l − 1 + B l \mathbf{Z}^l=(\mathbf{W}^{l-1})^T\mathbf{A}^{l-1}+\mathbf{B}^l Z l = ( W l − 1 ) T A l − 1 + B l A l = σ ( Z l ) \mathbf{A}^{l}=\sigma(\mathbf{Z}^l) A l = σ ( Z l ) A l − 1 ∈ R S l − 1 × n \mathbf{A}^{l-1}\in R^{S_{l-1}\times n} A l − 1 ∈ R S l − 1 × n B l ∈ R S l × 1 \mathbf{B}^l\in R^{S_l\times 1} B l ∈ R S l × 1 S l × n S_l\times n S l × n Z l ∈ R S l × n \mathbf{Z}^l\in R^{S_l\times n} Z l ∈ R S l × n W l − 1 ∈ R S l − 1 × S l \mathbf{W}^{l-1}\in R^{S_{l-1}\times S_l} W l − 1 ∈ R S l − 1 × S l i i i l − 1 l-1 l − 1 l l l i i i A l ∈ R S l × n \mathbf{A}^l\in R^{S_l\times n} A l ∈ R S l × n S l S_l S l l l l σ ( ⋅ ) \sigma(·) σ ( ⋅ ) s i g m o i d ( x ) = 1 1 + e x p ( − x ) sigmoid(x)=\frac{1}{1+exp(-x)} s i g m o i d ( x ) = 1 + e x p ( − x ) 1 r e l u ( x ) = m a x ( x , 0 ) relu(x)=max(x,0) r e l u ( x ) = m a x ( x , 0 ) t a n h ( x ) = 1 − e x p ( − 2 x ) 1 + e x p ( − 2 x ) tanh(x)=\frac{1-exp(-2x)}{1+exp(-2x)} t a n h ( x ) = 1 + e x p ( − 2 x ) 1 − e x p ( − 2 x )
编程实现:torch.nn.CrossEntropyLoss()),由于torch.utils.data.DataLoader迭代产生的批量样本数据的形状是(batch_size,dim),前述计算式中则是基于相反的形状,所以为了适用于已经定义好的d2l.train_ch3()等方法,我稍稍修改了该单隐层网络的前向传播计算式:Z n × S 2 2 = X n × S 1 W S 1 × S 2 1 + B 1 × S 2 2 \mathbf{Z}_{n\times S_2}^2=\mathbf{X}_{n\times S_1}\mathbf{W}_{S_1\times S_2}^1+\mathbf{B}_{1\times S_2}^2 Z n × S 2 2 = X n × S 1 W S 1 × S 2 1 + B 1 × S 2 2 A n × S 2 2 = σ ( Z n × S 2 2 ) \mathbf{A}_{n\times S_2}^2=\sigma(\mathbf{Z}_{n\times S_2}^2) A n × S 2 2 = σ ( Z n × S 2 2 ) Z n × S 3 3 = A n × S 2 2 W S 2 × S 3 2 + B 1 × S 3 3 \mathbf{Z}_{n\times S_3}^3=\mathbf{A}_{n\times S_2}^2\mathbf{W}_{S2\times S_3}^2+\mathbf{B}_{1\times S_3}^3 Z n × S 3 3 = A n × S 2 2 W S 2 × S 3 2 + B 1 × S 3 3 Y ^ = softmax ( Z n × S 3 3 ) \hat{\mathbf{Y}}=\sout{\textbf{softmax}}(\mathbf{Z}_{n\times S_3}^3) Y ^ = softmax ( Z n × S 3 3 )
准备数据 定义模型、损失和优化函数 训练 附(简洁实现) 仍使用Fashion-MNIST数据集,同Softmax多分类
首先定义激活函数,作为网络中的激活层:
1 2 3 4 5 6 7 8 import torch as ptdef sigmoid (Z ): return 1 /(1 +pt.exp(-Z)) def relu (Z ): return pt.max (Z,other=pt.Tensor([0.0 ])) def tanh (Z ): return (1 -pt.exp(-2 *Z))/(1 +pt.exp(-2 *Z))
优化函数当然还是简单的随机梯度下降,而将要调用的训练方法d2l.train_ch3()中已经定义了SGD过程:
1 2 3 4 5 6 7 8 def MLP_1 (X,W1,W2,B1,B2,activate ): X=X.view((-1 ,784 )) return activate(X.mm(W1)+B1).mm(W2)+B2 import torch.nn as nnloss=nn.CrossEntropyLoss()
训练前还是先准备数据生成器并作参数初始化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import d2lbatch_size=256 train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size,root='./data/FashionMNIST' ) num_inputs=784 num_hiddens=256 num_outputs=10 W1 = pt.tensor(np.random.normal(0 , 0.01 , (num_inputs, num_hiddens)), dtype=pt.float ) B1 = pt.zeros(num_hiddens, dtype=pt.float ) W2 = pt.tensor(np.random.normal(0 , 0.01 , (num_hiddens, num_outputs)), dtype=pt.float ) B2 = pt.zeros(num_outputs, dtype=pt.float ) params = [W1, B1, W2, B2] for param in params: _=param.requires_grad_(requires_grad=True )
开始训练:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 from functools import partialnum_epochs = 5 lr = 100.0 net = partial(MLP_1,W1=W1,W2=W2,B1=B1,B2=B2,activate=relu) d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr) '''OUTPUT epoch 1, loss 0.0030, train acc 0.709, test acc 0.737 epoch 2, loss 0.0019, train acc 0.824, test acc 0.787 epoch 3, loss 0.0017, train acc 0.845, test acc 0.795 epoch 4, loss 0.0016, train acc 0.855, test acc 0.854 epoch 5, loss 0.0015, train acc 0.864, test acc 0.816 '''
train_iter,test_iter,loss都复用自前面的代码,此处简洁实现只要重新定义网络部分即可:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 num_inputs, num_outputs, num_hiddens = 784 , 10 , 256 net=nn.Sequential( d2l.FlattenLayer(), nn.Linear(num_inputs,num_hiddens), nn.ReLU(), nn.Linear(num_hiddens,num_outputs) ) from torch.nn import initfor params in net.parameters(): _=init.normal_(params, mean=0 , std=0.01 ) optimizer = pt.optim.SGD(net.parameters(), lr=0.5 ) num_epochs = 5 d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None , None , optimizer) '''OUTPUT epoch 1, loss 0.0030, train acc 0.708, test acc 0.700 epoch 2, loss 0.0019, train acc 0.821, test acc 0.745 epoch 3, loss 0.0017, train acc 0.842, test acc 0.829 epoch 4, loss 0.0015, train acc 0.856, test acc 0.858 epoch 5, loss 0.0014, train acc 0.865, test acc 0.846 '''
![图2. 线性回归是一个单层(感知器)神经网络[3]](https://cdn.statically.io/gh/celestezj/ImageHosting/master/img/20210608151347.png)
![图4. Softmax多分类模型是一个单层(感知器)神经网络[3]](https://cdn.statically.io/gh/celestezj/ImageHosting/master/img/20210609155526.png)

![图6. 由单个隐层构成的多层感知器[3]](https://cdn.statically.io/gh/celestezj/ImageHosting/master/img/20210611092144.png)